周波数領域適応雑音キャンセリング

公開日: 2015年11月25日 · 最終更新日: 2025年8月8日

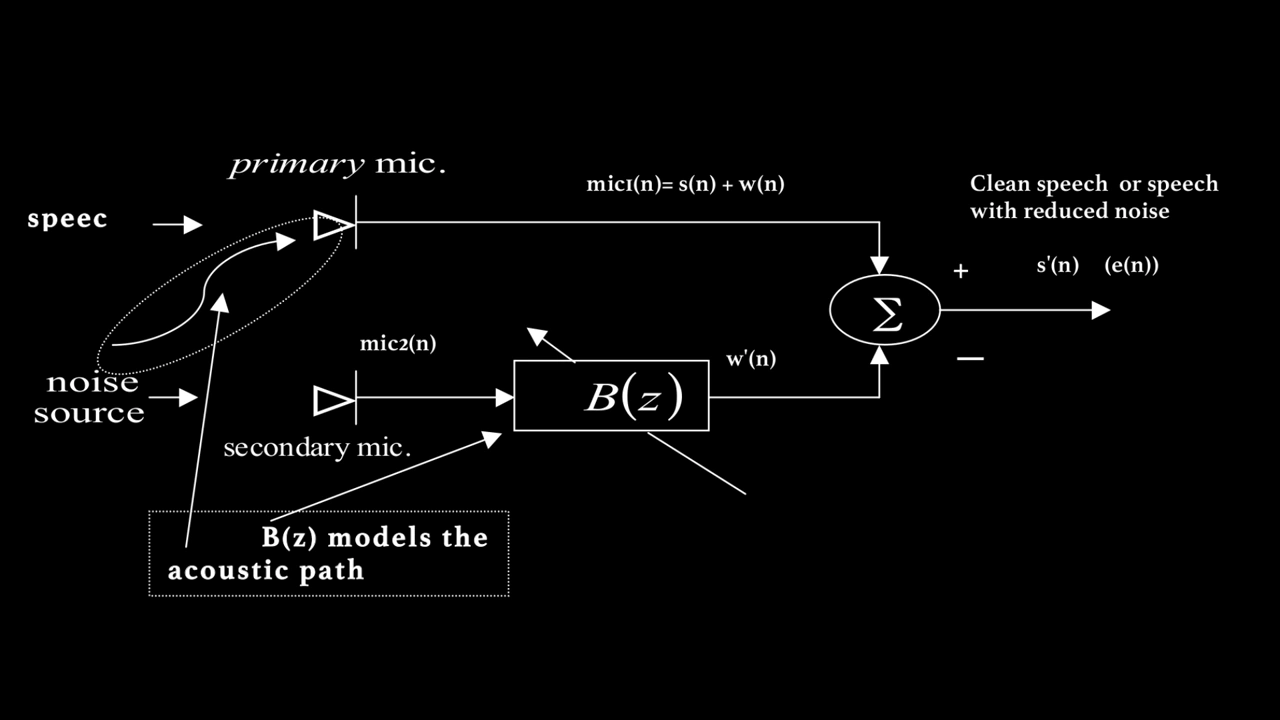システム構成図 図1: 適応雑音キャンセラー

概要

適応フィルターとは、誤差を最小化しリアルタイムで目的の信号をモデル化するために、最小平均二乗法（LMS）などのアルゴリズムを用いて係数を自動調整する自己適応型のデジタルフィルターです。固定フィルターとは異なり、入力条件の変化に継続的に適応するため、雑音キャンセリング、エコー抑制、システム同定、信号予測などの応用で広く使われています。本プロジェクトでは、NLMSアルゴリズムを用いた適応フィルターを使い、音声＋背景雑音が混在する信号から雑音を除去することを試みます。

モデル

図1はモデル化する適応雑音キャンセラーのシステム図を示しています。このシステムは2つのマイクを使用します。

Mic1 はスピーカーの近くに配置されます。きれいな音声を拾いますが、不要な背景雑音も含まれます。
Mic2 はスピーカーから離れ、雑音源に近い場所に配置されます。

目標は、Mic2で拾った雑音を利用してMic1の雑音成分を除去し、よりクリーンな音声信号を得ることです。

しかし、Mic1の雑音はMic2の雑音と同一ではありません。雑音源からMic1への音響経路の影響で、Mic1の雑音には反射、遅延、その他の歪みが含まれる可能性があります。したがって、単純にMic2の信号をMic1から引くだけでは不十分です。

これを解決するために、FIRフィルター $B(z)$ を用いて、Mic2からの雑音がMic1に現れる様子をモデル化します。 $B(z)$ の係数は**正規化最小二乗法（NLMS）**アルゴリズムで継続的に更新されます。

主マイクの信号は以下です:

$s(n) + w(n)$

ここで:

$n$ は時間インデックス、
$s(n)$ はクリーンな音声信号、
$w(n)$ はMic1の雑音。

雑音除去後の出力信号は:

$s(n) + w(n) - w'(n)$

ここで $w'(n)$ はMic2の信号を $B(z)$ でフィルタリングした推定雑音です。

アルゴリズム

主マイクと副マイクから音声を読み込む。
サイズ $N$ のフレームを取り出し、スペクトル漏れを減らすために窓関数（例：ハニング窓）を適用。
DFTを実行:
- DFTの周波数分解能を上げるためにゼロパディングを使用。
- フレームを円環的にシフトし中心をインデックス0に合わせることで、ゼロ位相窓を適用し位相オフセットを防止。対称窓 $w[n]$ のフーリエ変換は実数値となり、 $X$ の位相変化を避ける。
周波数領域での雑音推定:
$Y = B \cdot X$ ここで $B$ は適応フィルター、 $X$ はMic2のスペクトラム。
主マイクから雑音を差し引く:
$E = D - Y$ ここで $D$ はMic1のスペクトラム、 $E$ は誤差信号（クリーン信号）。
正規化LMSを用いてフィルター係数を更新:
$B \mathrel{+}= \frac{2 \mu \cdot \mathrm{conj}(X) \cdot E}{|X|^2 + \varepsilon}$ ここで $B$ は係数、 $X$ はMic2スペクトラム、 $E$ は誤差信号、 $\mu$ はステップサイズ、 $\varepsilon$ は数値安定化のための微小定数。
逆FFTをかけ、オーバーラップ・アドで時間領域信号を再構成。
ステップ2～7を音声終端まで繰り返す（ホップサイズ分ずつフレームを進める）。
正規化してクリーン信号と分離雑音の両方を出力。

パラメーター

フレームサイズ ( $N$ )
各分析フレームの長さを決定。

ホップサイズ (hop_size) 次のフレームへ進むサンプル数（フレームシフト）。

ステップサイズ ( $\mu$ )
フィルター係数の適応速度を制御:

小さい $\mu$ : 適応は遅いが安定。変化にゆっくり反応し、過剰反応しにくい。
大きい $\mu$ : 適応は速いが不安定になりやすく、フィルターが急激な変化に過剰反応し「プリエコー」「ポストエコー」などのアーティファクトを引き起こす可能性あり。

イプシロン ( $\epsilon$ )
計算時の数値安定化のための小さい定数（0除算防止）。

窓関数 ( $window$ )
各フレームに適用しスペクトル漏れを減らす窓の種類。

フィルター係数 ( $B$ )
時間経過で適応される初期係数。

コード

import numpy as np
import soundfile as sf
from scipy.fft import fft, ifft
from scipy.signal.windows import hann
import matplotlib.pyplot as plt
# === 補助関数 ===
def moving_average(x, w):
    return np.convolve(x, np.ones(w)/w, mode='valid')

# === 信号の読み込み ===
mic1, fs = sf.read("mic1_noise.wav")  # 音声＋雑音
mic2, _  = sf.read("mic2_noise.wav")  # 雑音参照

# === パラメーター ===
N = 512            # FFT/フレームサイズ
hop_size = N // 2   # 50%オーバーラップ
mu = 0.0015         # ステップサイズ（小さいほど安定）
eps = 1e-6          # 数値安定化用
window = hann(N)
B = np.zeros(N, dtype=complex)

# 長さを揃える
length = min(len(mic1), len(mic2))
mic1 = mic1[:length]
mic2 = mic2[:length]

# === 初期化 ===
output = np.zeros(length + N)
weight = np.zeros(length + N)
error_db = []
snr_db = []

# === 適応ループ ===
for i in range(0, length - N, hop_size):
    frame_i = slice(i, i + N)

    # Mic1とMic2の入力フレームに窓をかける
    d = mic1[frame_i] * window
    x = mic2[frame_i] * window

    # FFT計算
    D = fft(d)
    X = fft(x)

    # 周波数領域で雑音推定 (Y)
    Y = B * X

    # 主マイク信号から雑音を差し引く
    E = D - Y

    # 正規化LMSでフィルター係数更新
    B += 2 * mu * np.conj(X) * E / (np.abs(X)**2 + eps) 

    # 逆FFTして時間領域に戻す
    e = np.real(ifft(E)) * window

    # オーバーラップ・アド
    output[i:i+N] += e
    weight[i:i+N] += window**2

    # エラー・SNR計算
    error_power = np.sum(np.abs(E)**2)
    signal_power = np.sum(np.abs(D)**2)
    error_db.append(10 * np.log10(error_power + eps))
    snr_db.append(10 * np.log10(signal_power / (error_power + eps)))

# === 出力正規化 ===
nonzero = weight > 1e-6
output[nonzero] /= weight[nonzero]
output = output[:length]

peak = np.max(np.abs(output))
if peak > 1e-6:
    output /= peak

# === 結果保存 ===
np.save('B.npy', B) # 最終フィルター係数
sf.write("output.wav", output, fs)

# === 収束曲線のプロット ===
plt.figure(figsize=(10, 5))

# エラー収束
plt.subplot(2, 1, 1)
plt.plot(moving_average(error_db, w=64))
plt.title("収束曲線（誤差パワー dB）")
plt.xlabel("フレームインデックス")
plt.ylabel("誤差パワー (dB)")
plt.grid(True)

# SNR改善
plt.subplot(2, 1, 2)
plt.plot(moving_average(snr_db, w=64))
plt.title("時間経過によるSNR")
plt.xlabel("フレームインデックス")
plt.ylabel("SNR (dB)")
plt.grid(True)

plt.tight_layout()
plt.show()

出力

オーディオサンプル

マイク1からの入力音声

マイク2からの入力音声

1回目の処理後の出力音声

2回目の処理後の出力音声

適応ノイズフィルターが出力音声のノイズを徐々に除去しているのが聞こえます。フィルター係数 $B(z)$ は初回処理時に初期化されているため、ノイズキャンセリングの効果がより高まっています。

性能評価

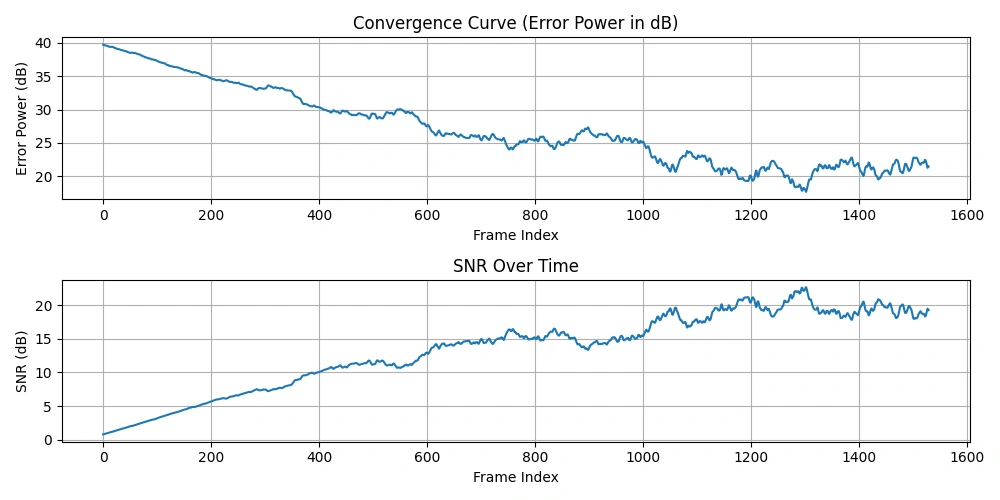図2：収束曲線と時間経過に伴うSNRのプロット

収束曲線（エラーパワー[dB]）

$\mathrm{errorPower} = \sum_{n=1}^{N} |E(n)|^2$

$\text{エラーパワー（dB）} = 10 \log_{10}\bigl(\mathrm{errorPower} + \varepsilon\bigr)$

この曲線は、適応フィルターがノイズキャンセルを学習するにつれて、エラーパワー（残留ノイズのエネルギー）が時間とともにどのように減少するかを示しています。

フレームごとの信号対雑音比（SNR）

$\mathrm{signalPower} = \sum_{n=1}^{N} |D(n)|^2$

$\mathrm{errorPower} = \sum_{n=1}^{N} |E(n)|^2$

$\mathrm{SNR} = 10 \log_{10} \left( \frac{\mathrm{signalPower}}{\mathrm{errorPower} + \varepsilon} \right)$

ここで：

信号パワー = $|D|^2$ （一次マイクのフレームスペクトルのパワー）
エラーパワー = $|E|^2$ （キャンセル後の残留ノイズのパワー）

SNRは通常、適応フィルターがノイズ抑制を改善するにつれて時間とともに増加します。

移動平均

これらの曲線に移動平均を適用することで、変動が平滑化され、全体的な傾向が見やすくなります。

エラーパワーの収束曲線は、ノイズエネルギーがどれほど効果的に減少したかを示します（減少するべき）。
SNR曲線は、信号の明瞭さがノイズに対してどのように改善したかを示します（増加するべき）。

この逆の関係は直感的に理解できます。フィルターがノイズをより正確に推定しキャンセルするほど、残留エラーが減り、SNRが向上します。

主要な概念のまとめ

周波数成分 $B(k)$ は適応フィルターの周波数応答を表し、二次マイクで捉えたノイズが一次マイクのノイズをキャンセルするためにどのように変換されているかを示しています。FFTサイズ $N$ を大きくすると周波数分解能が上がり、より正確なノイズモデルが可能になり、SNRが向上することがあります。しかし、 $N$ が大きいとレイテンシーが増え、フィルターの適応が遅くなります。

FFTサイズ $N$ とフィルター次数には直接の関係があり、大きなFFTはより長いフィルターに対応し、複雑な音響経路や長いインパルス応答をモデル化できます。ステップサイズ $\mu$ はフィルター適応の速度と安定性を制御し、小さい値は遅く安定した適応をもたらし、歪みを最小限に抑えます。一方で大きい値は速い適応を可能にしますが、歪みや音楽ノイズ、プリエコー／ポストエコーなどのアーティファクトを引き起こすリスクがあります。

一般的に、SNRが高いほど音声品質は良好に感じられますが、過度なノイズキャンセリングは聴覚的に不快なアーティファクトを生む場合があります。エラー信号 $e(n)$ を最小化することは、フィルターがノイズをどれだけ効果的にキャンセルしているかを反映し、音声の明瞭さを向上させるために重要です。フィルターの時間領域の挙動を理解するには、 $B(k)$ の逆FFTを計算し、周波数領域の係数をインパルス応答に変換します。

結論

周波数領域の適応フィルターは、一次マイクの信号からノイズスペクトルをモデル化して差し引くことで効果的にノイズをキャンセルします。FFTアルゴリズムを利用した周波数領域処理は、特に長いFIRフィルターにおいて計算効率を高めます。正規化LMSアルゴリズムは、基準信号のパワーに応じてステップサイズを正規化し、発散の可能性を減らして安定した適応を実現します。

ステップサイズ $\mu$ の選択はトレードオフであり、小さい $\mu$ は収束が遅いが安定、大きい $\mu$ は高速適応だが不安定でアーティファクト発生のリスクがあります。窓関数処理やゼロ位相整合技術によりスペクトルリーケージや位相歪みを抑え、フィルター性能を向上させます。オーバーラップ加算法により、ギャップや不連続のない滑らかな出力信号が保証されます。

将来的な改良として、再帰最小二乗（RLS）法、適応的ステップサイズ制御、多数マイクアレイの活用などの高度な適応手法の導入が考えられます。リアルタイム実装にはさらなる最適化が必要ですが、この周波数領域アプローチはオフライン・リアルタイム両方のデジタル信号処理における適応ノイズキャンセリングの強固な基盤となります。